Modèle IS-LM II
TD Introduction à la macroéconomie
2025-05-06
Rappels de cours
Modèle IS-LM - Une approche plus macro
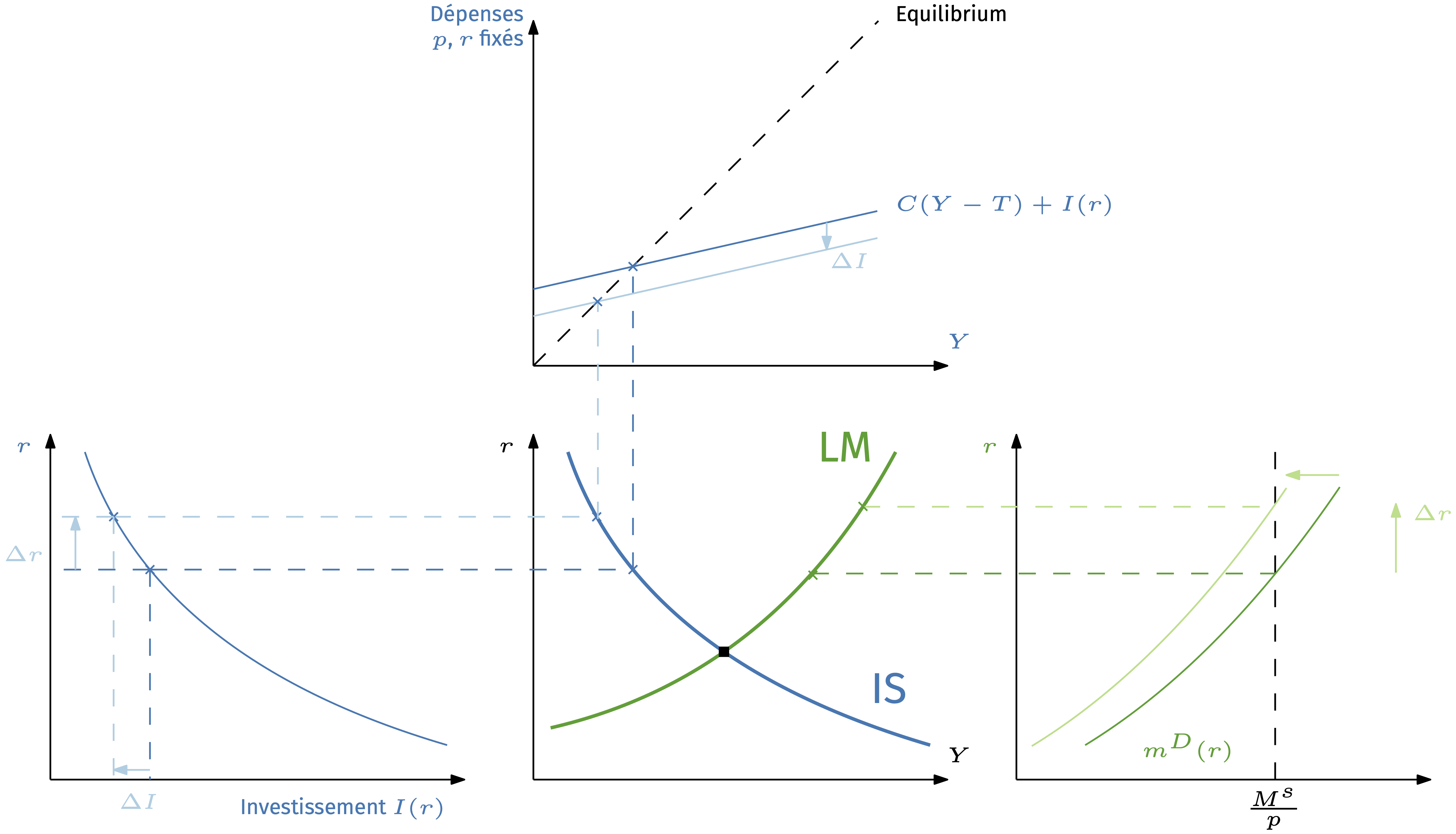
Modèle IS-LM - Retour à l’approche micro
Les marchés des biens (pour chaque période), du travail et de la monnaie doivent s’équilibrer :
- Marché des biens, période 1 : \(Y_{1} = C_{1} + K\)
- Marché des biens, période 2 : \(C_{2} = F_{2}(K)\)
- Marché du travail : \(L = F_{1}^{-1}(Y_{1})\) (le travail s’ajuste à la demande)
- Marché de la monnaie : \(M^{S} = m^{D}(Y_{1},i)p_{1}\)
On dérive les deux équations suivantes :
- IS: \(u^{\prime}\left(Y_{1}-K\left(i-\pi\right)\right)=\beta\left(1+i-\pi\right)u^{\prime}\left(F_{2}\left(K\left(i-\pi\right)\right)\right)\)
- LM: \(M^{S} = m^{D}(Y_{1},i)p_{1}\)
Exercice 2 – Effet de l’investissement
Modèle néo‑keynésien simplifié avec investissement exogène et
\[
F_2(K)=\min\{A\,K,\,A\bar K\},
\]
utilité \(u(c)=\ln(c)\), \(\beta=1\), \(\pi=0\).
- Dérivez l’équation IS, c’est‑à‑dire la relation \(Y_1(i)\) pour paramètres exogènes \(A,\bar K\).
- En \(i\) fixe, de combien \(Y_1\) augmente quand \(\bar K\) croît d’une unité ? Pourquoi cela dépend‑il de \(A\) ?
- Ancienne version : \(c(Y_1)=a+bY_1\) et même \(F_2(K)\). Trouvez \(Y_1(a,b,A,\bar K)\) par l’équilibre marché des biens. Pourquoi pas de dépendance en \(i\) ?
- De combien \(Y_1\) change quand \(\bar K\) augmente ? Pourquoi dépend‑ceci de \(b\) mais pas de \(A\), et pourquoi diffère‑t‑il de la question 2 ?
Exercice 3 – Une récession
Données 2035 vs 2036 :
| 2035 | 2036 | |
|---|---|---|
| \(K\) | 10000 | 10000 |
| \(L\) | 1 | 0,81 |
| \(Y\) | 4000 | 3600 |
| \(w\) | 2000 | 1800 |
| \(r^K\) | 2000 | 1800 |
| \(I\) | 800 | 600 |
| \(c\) | 3200 | 3000 |
| \(p\) | 100 | 90 |
| \(i_{nom}\) | 5 % | 10 % |
- Proposez deux causes de récession incompatibles avec ces données. Pour chacune :
- Pourquoi ce canal peut‑il baisser \(Y\) ?
- Qu’indiquent les données contre cette explication ?
- Pourquoi ce canal peut‑il baisser \(Y\) ?
- Trouvez une cause compatible avec les chiffres. Expliquez pourquoi le modèle la rend plausible et quelle donnée la valide.
Exercice 4 – Inflation future et inflation présente
Dans un cadre néo‑keynésien à prix rigides, \(\pi_1\) est l’inflation entre t=0→1, \(\pi_2\) entre 1→2, toutes deux exogènes. Si \(\pi_2\) augmente (ex. hausse de \(M^s\)), que fait \(\pi_1\) ? Décrivez les étapes du raisonnement.
Exercice 5 – Politique budgétaire vs. politique monétaire
Guerre chars USA vs Canada, prix rigides.
- Si la Fed garde \(M^s\) constant :
- Effet sur \(Y\) ?
- Sur taux nominaux \(i\) ?
- Sur niveau des prix \(P\) ?
- Effet sur \(Y\) ?
- Si la Fed ajuste \(M^s\) pour maintenir \(i\) constant :
- Que fait‐elle sur \(M^s\) ?
- Impact sur \(Y\) vs (1) ?
- Impact sur \(P\) vs (1) ?
- Que fait‐elle sur \(M^s\) ?
- Si la Fed cible strictement \(\pi\) :
- Que fait‐elle sur \(M^s\) ?
- Impact sur \(Y\) vs (1) ?
- Impact sur \(i\) vs (1) ?
- Que fait‐elle sur \(M^s\) ?
Exercice 6 – Consommation patriotique
Le Président appelle à consommer, un ménage achète une tondeuse.
- Proposez un modèle où cet appel nuit au bien‑être. Décrivez précisément le mécanisme.
- Proposez un modèle où cet appel est bénéfique. Décrivez précisément le mécanisme.
Exercice 7 – Impôts et inflation
Prix rigides, la Fed ne bouge pas. Deux impôts temporaires rapportant même recette :
- Forfaitaire \(\Delta\) par ménage
- Taxe proportionnelle à la consommation
- Si \(G_{t}\) et \(G_{t+1}\) inchangés, à quoi les ménages s’attendent‑ils pour \(T_{t+1}\) ?
- L’un ou l’autre plan réduit‑il \(\pi\) ? Quel canal ? Sinon, pourquoi ?
- Si beaucoup de ménages sont contraints par leur accès au crédit, quel impact sur votre réponse ?
Papier scientifique de la semaine
Rappels sur les RBC
\[\begin{align} \max_{c_1, c_2, l, L, K} \quad & u(c_1) + v(l) + \beta u(c_2) \\ \text{s.t.} \quad & c_1 + K = Y_1 \\ & Y_1 = F_1(L) \\ & c_2 = F_2(K) \\ & L = 1 - l \end{align}\]
\[Y_1 = F_1(L)\]
\[\frac{v'(1-L)}{u'(c_1)} = F'_1(L)\]
\[u'(c_1) = \beta F'_2(K)u'(F_2(K))\]
\[Y_1 = (u')^{-1}[\beta F'_2(K)u'(F_2(K))] + K\]
Modèle IS-LM
#| '!! shinylive warning !!': |
#| shinylive does not work in self-contained HTML documents.
#| Please set `embed-resources: false` in your metadata.
#| standalone: true
#| viewerHeight: 650
from shiny import App, ui, reactive, render_plot
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import root_scalar
# -- Functional forms --
# CRRA utility: u(c) = c^(1-sigma)/(1-sigma) => u'(c) = c^(-sigma)
# Production in period 2: F2(K) = A2 * K^alpha2
# Investment condition: F2'(K) = alpha2 * A2 * K^(alpha2-1) = 1 + r => K(r)
# Money demand: mD(Y,i) = Y / i (real money demand)
alpha1, alpha2 = 0.7, 0.3
p1 = 1.0 # price level period 1
def marginal_util(c, sigma):
return c**(-sigma)
def K_of_r(r, A2):
# invert F2'(K)=1+r
return ((1 + r) / (alpha2 * A2))**(1/(alpha2 - 1))
# IS: for a given Y, solve u'(c1) - beta*(1+r)*u'(c2) = 0, where c1=Y-K, c2=F2(K)
def compute_i_IS(Y, beta, A, A2, pi, sigma):
def f_root(r):
K = K_of_r(r, A2)
c1 = Y - K
c2 = A2 * K**alpha2
return marginal_util(c1, sigma) - beta*(1+r)*marginal_util(c2, sigma)
# find bracket [r_lo, r_hi] where f_root changes sign
r_vals = np.linspace(-0.9, 10, 200)
f_vals = [f_root(r) for r in r_vals]
bracket = None
for i in range(len(r_vals)-1):
if f_vals[i] * f_vals[i+1] < 0:
bracket = (r_vals[i], r_vals[i+1])
break
if bracket is None:
# fallback to secant if no bracket found
sol = root_scalar(f_root, x0=0.1, x1=1.0, method='secant', maxiter=100)
else:
sol = root_scalar(f_root, bracket=bracket, method='bisect', maxiter=100)
r_star = sol.root
return r_star + pi
# LM: solve M_s/p1 - Y/i = 0 => i = Y * p1 / M_s
def compute_i_LM(Y, M_s):
return Y * p1 / M_s
# -- UI --
app_ui = ui.page_fluid(
ui.h2("IS-LM with Exact Equations"),
ui.layout_sidebar(
ui.sidebar(
ui.input_slider("A", "Productivity A (F1 scale):", min=0.5, max=2.0, value=1.0, step=0.1),
ui.input_slider("A2", "Optimism A2 (F2 scale):", min=0.5, max=2.0, value=1.0, step=0.1),
ui.input_slider("beta", "Discount β:", min=0.1, max=1.0, value=0.98, step=0.01),
ui.input_slider("sigma","CRRA σ:", min=0.5, max=5.0, value=2.0, step=0.1),
ui.input_slider("Ms", "Money Supply M^S:", min=0.5, max=5.0, value=1.0, step=0.1),
ui.input_slider("pi", "Inflation π:", min=0.0, max=0.5, value=0.02, step=0.01),
ui.input_action_button("reset", "Reset Defaults")
),
ui.card(
ui.card_header("IS & LM Diagram"),
ui.card_body(ui.output_plot("plot", height="600px"))
)
)
)
# -- Server --
def server(input, output, session):
# store initial defaults
DEFAULTS = {
"A": 1.0,
"A2": 1.0,
"beta": 0.98,
"sigma":2.0,
"Ms": 1.0,
"pi": 0.02
}
# reset sliders to initial defaults when button is pressed
@reactive.event(input.reset)
def _reset_inputs():
for name, val in DEFAULTS.items():
session.set_input_value(name, val)
@output
@render_plot()
def plot():
# Base parameters
A0, A20, beta0, sigma0, Ms0, pi0 = 1.0, 1.0, 0.98, 2.0, 1.0, 0.02
# Current
A, A2, beta, sigma, Ms, pi = (
input.A(), input.A2(), input.beta(), input.sigma(), input.Ms(), input.pi()
)
# Y grid
Y = np.linspace(0.1, 10, 100)
# Compute curves
i_IS_base = [compute_i_IS(y, beta0, A0, A20, pi0, sigma0) for y in Y]
i_LM_base = compute_i_LM(Y, Ms0)
i_IS_cur = [compute_i_IS(y, beta, A, A2, pi, sigma) for y in Y]
i_LM_cur = compute_i_LM(Y, Ms)
# Equilibrium for current
eq_diff = np.abs(np.array(i_IS_cur) - np.array(i_LM_cur))
idx = eq_diff.argmin()
Y_eq, i_eq = Y[idx], i_IS_cur[idx]
# Plot
fig, ax = plt.subplots(figsize=(8,6))
# base curves
ax.plot(Y, i_IS_base, '--', color='gray', alpha=0.5, label='IS (base)')
ax.plot(Y, i_LM_base, '--', color='gray', alpha=0.5, label='LM (base)')
# current curves
ax.plot(Y, i_IS_cur, '-', color='crimson', label='IS (current)')
ax.plot(Y, i_LM_cur, '-', color='navy', label='LM (current)')
# equilibrium
ax.plot(Y_eq, i_eq, 'ko')
ax.axhline(i_eq, linestyle='--', color='black')
ax.axvline(Y_eq, linestyle='--', color='black')
ax.text(Y_eq, i_eq, f' (Y*, i*)=({Y_eq:.2f},{i_eq:.2f})')
ax.set_xlabel('Output Y')
ax.set_ylabel('Interest rate i')
ax.set_title('Exact IS-LM Curves')
ax.legend()
ax.grid(True)
return fig
app = App(app_ui, server)