Modèle IS-LM
TD Introduction à la macroéconomie
2025-04-29
Rappels de cours
Rappels sur les RBC
\[\begin{align} \max_{c_1, c_2, l, L, K} \quad & u(c_1) + v(l) + \beta u(c_2) \\ \text{s.t.} \quad & c_1 + K = Y_1 \\ & Y_1 = F_1(L) \\ & c_2 = F_2(K) \\ & L = 1 - l \end{align}\]
\[Y_1 = F_1(L)\]
\[\frac{v'(1-L)}{u'(c_1)} = F'_1(L)\]
\[u'(c_1) = \beta F'_2(K)u'(F_2(K))\]
\[Y_1 = (u')^{-1}[\beta F'_2(K)u'(F_2(K))] + K\]
TD6 - Exercice 5 - Bonne nouvelle
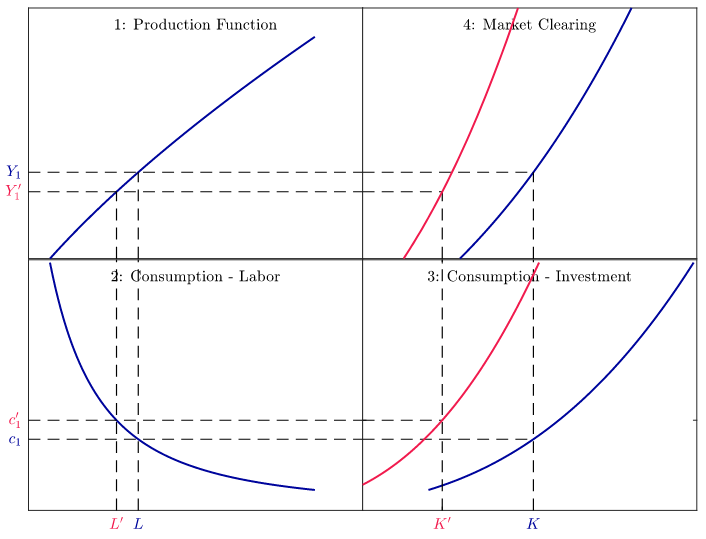
Considérez le modèle RBC à deux périodes, résumé par les équations (1) à (4). Supposez que le ménage représentatif développe une forme très particulière d’optimisme quant à l’avenir. Il estime que la fonction de production de la période 2 est :
\[Y_2 = F_2(K) + A\]
En quoi ce type d’optimisme diffère-t-il de celui étudié en cours ?
Qu’adviendra-t-il de l’emploi, de la production, de la consommation, de l’investissement, des salaires et du taux d’intérêt réel ?
Ce type d’optimisme produit-il quelque chose qui ressemble à un cycle économique? Pourquoi ?
TD6 - Exercice 5 - Bonne nouvelle
TD6 - Exercice 6 - Dépenses publiques
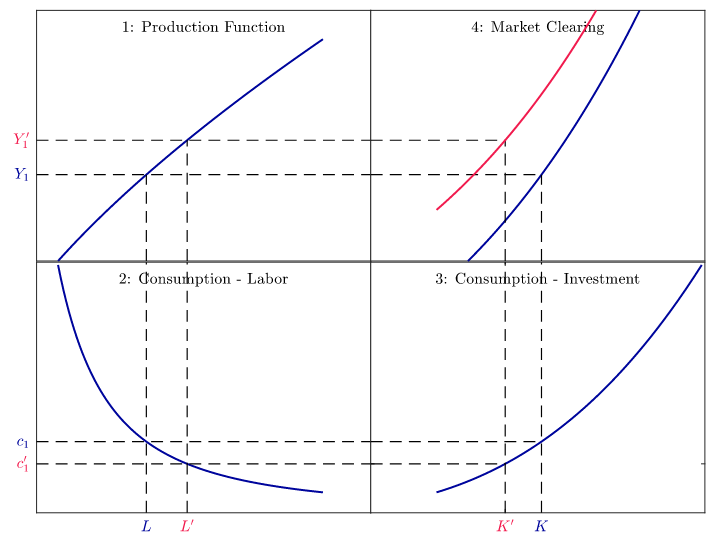
Considérez une économie bien décrite par le modèle RBC, avec une modification près : un gouvernement dépense \(G\) à la période 1. Il finance ces dépenses en prélevant des impôts forfaitaires auprès du ménage représentatif (l’équivalence ricardienne est vérifiée, il n’est donc pas nécessaire de préciser quand le gouvernement perçoit ces impôts). G n’entre pas dans la fonction d’utilité du ménage représentatif.
Où \(G\) apparaîtrait-il dans le système d’équations (1)-(4) ? Expliquez.
Supposez une augmentation de \(G\). Qu’advient-il de la production, de la consommation, de l’emploi et de l’investissement ? Qu’advient-il des salaires et des taux d’intérêt ? Représentez-le graphiquement et expliquez ce qui se passe.
TD6 - Exercice 6 - Dépenses publiques
Exercice 1 – Trop de clients
J&J est un fabricant de shampoing. Son service d’ingénierie estime que s’il décide de produire \(q\) unités de shampoing, le coût total est
\[
c(q) = a\,q + 2b\,q^2.
\]
Son service marketing prévoit la demande
\[
q(p)=\alpha - \beta\,p,
\]
avec \(\alpha/\beta > a\).
- Quel prix \(p\) maximise le profit de J&J ?
- Supposons que J&J fixe ce prix, puis découvre que la demande réelle est
\[ q(p)=\alpha' - \beta\,p,\quad \alpha'>\alpha. \]
S’il satisfait toutes les commandes, combien d’unités vendra-t-il ? Comment cela dépend-il de \(\alpha\) et \(\alpha'\) ?
- Pour quelles valeurs de \(\alpha'\) J&J aurait‑il intérêt à refuser certains clients ?
- Si la demande était correcte mais que les coûts sont
\[ c(q)=a'\,q+2b\,q^2,\quad a'>a, \]
pour quelles valeurs de \(a'\) J&J refuserait‑il des clients ?
Exercice 2 – Effet de l’investissement
Modèle néo‑keynésien simplifié avec investissement exogène et
\[
F_2(K)=\min\{A\,K,\,A\bar K\},
\]
utilité \(u(c)=\ln(c)\), \(\beta=1\), \(\pi=0\).
- Dérivez l’équation IS, c’est‑à‑dire la relation \(Y_1(i)\) pour paramètres exogènes \(A,\bar K\).
- En \(i\) fixe, de combien \(Y_1\) augmente quand \(\bar K\) croît d’une unité ? Pourquoi cela dépend‑il de \(A\) ?
- Ancienne version : \(c(Y_1)=a+bY_1\) et même \(F_2(K)\). Trouvez \(Y_1(a,b,A,\bar K)\) par l’équilibre marché des biens. Pourquoi pas de dépendance en \(i\) ?
- De combien \(Y_1\) change quand \(\bar K\) augmente ? Pourquoi dépend‑ceci de \(b\) mais pas de \(A\), et pourquoi diffère‑t‑il de la question 2 ?
Exercice 3 – Une récession
Données 2035 vs 2036 :
| 2035 | 2036 | |
|---|---|---|
| \(K\) | 10000 | 10000 |
| \(L\) | 1 | 0,81 |
| \(Y\) | 4000 | 3600 |
| \(w\) | 2000 | 1800 |
| \(r^K\) | 2000 | 1800 |
| \(I\) | 800 | 600 |
| \(c\) | 3200 | 3000 |
| P | 100 | 90 |
| i_nom | 5 % | 10 % |
- Proposez deux causes de récession incompatibles avec ces données. Pour chacune :
- Pourquoi ce canal peut‑il baisser \(Y\) ?
- Qu’indiquent les données contre cette explication ?
- Pourquoi ce canal peut‑il baisser \(Y\) ?
- Trouvez une cause compatible avec les chiffres. Expliquez pourquoi le modèle la rend plausible et quelle donnée la valide.
Modèle IS-LM
Les marchés des biens (pour chaque période), du travail et de la monnaie doivent s’équilibrer :
- Marché des biens, période 1 : \(Y_{1} = C_{1} + K\)
- Marché des biens, période 2 : \(C_{2} = F_{2}(K)\)
- Marché du travail : \(L = F_{1}^{-1}(Y_{1})\) (le travail s’ajuste à la demande)
- Marché de la monnaie : \(M^{S} = m^{D}(Y_{1},i)p_{1}\)
On dérive les deux équations suivantes :
- IS: \(u^{\prime}\left(Y_{1}-K\left(i-\pi\right)\right)=\beta\left(1+i-\pi\right)u^{\prime}\left(F_{2}\left(K\left(i-\pi\right)\right)\right)\)
Si les taux montent, investir coûte plus cher → les entreprises réduisent l’investissement → la demande globale baisse → le PIB baisse.
- LM: \(M^{S} = m^{D}(Y_{1},i)p_{1}\)
Si le PIB augmente, les gens veulent plus de monnaie → pour que la demande de monnaie reste compatible avec l’offre fixe, les taux doivent augmenter.
Modèle IS-LM
#| '!! shinylive warning !!': |
#| shinylive does not work in self-contained HTML documents.
#| Please set `embed-resources: false` in your metadata.
#| standalone: true
#| viewerHeight: 650
from shiny import App, ui, reactive, render_plot
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import root_scalar
# -- Functional forms --
# CRRA utility: u(c) = c^(1-sigma)/(1-sigma) => u'(c) = c^(-sigma)
# Production in period 2: F2(K) = A2 * K^alpha2
# Investment condition: F2'(K) = alpha2 * A2 * K^(alpha2-1) = 1 + r => K(r)
# Money demand: mD(Y,i) = Y / i (real money demand)
alpha1, alpha2 = 0.7, 0.3
p1 = 1.0 # price level period 1
def marginal_util(c, sigma):
return c**(-sigma)
def K_of_r(r, A2):
# invert F2'(K)=1+r
return ((1 + r) / (alpha2 * A2))**(1/(alpha2 - 1))
# IS: for a given Y, solve u'(c1) - beta*(1+r)*u'(c2) = 0, where c1=Y-K, c2=F2(K)
def compute_i_IS(Y, beta, A, A2, pi, sigma):
def f_root(r):
K = K_of_r(r, A2)
c1 = Y - K
c2 = A2 * K**alpha2
return marginal_util(c1, sigma) - beta*(1+r)*marginal_util(c2, sigma)
# find bracket [r_lo, r_hi] where f_root changes sign
r_vals = np.linspace(-0.9, 10, 200)
f_vals = [f_root(r) for r in r_vals]
bracket = None
for i in range(len(r_vals)-1):
if f_vals[i] * f_vals[i+1] < 0:
bracket = (r_vals[i], r_vals[i+1])
break
if bracket is None:
# fallback to secant if no bracket found
sol = root_scalar(f_root, x0=0.1, x1=1.0, method='secant', maxiter=100)
else:
sol = root_scalar(f_root, bracket=bracket, method='bisect', maxiter=100)
r_star = sol.root
return r_star + pi
# LM: solve M_s/p1 - Y/i = 0 => i = Y * p1 / M_s
def compute_i_LM(Y, M_s):
return Y * p1 / M_s
# -- UI --
app_ui = ui.page_fluid(
ui.h2("IS-LM with Exact Equations"),
ui.layout_sidebar(
ui.sidebar(
ui.input_slider("A", "Productivity A (F1 scale):", min=0.5, max=2.0, value=1.0, step=0.1),
ui.input_slider("A2", "Optimism A2 (F2 scale):", min=0.5, max=2.0, value=1.0, step=0.1),
ui.input_slider("beta", "Discount β:", min=0.1, max=1.0, value=0.98, step=0.01),
ui.input_slider("sigma","CRRA σ:", min=0.5, max=5.0, value=2.0, step=0.1),
ui.input_slider("Ms", "Money Supply M^S:", min=0.5, max=5.0, value=1.0, step=0.1),
ui.input_slider("pi", "Inflation π:", min=0.0, max=0.5, value=0.02, step=0.01),
ui.input_action_button("reset", "Reset Defaults")
),
ui.card(
ui.card_header("IS & LM Diagram"),
ui.card_body(ui.output_plot("plot", height="600px"))
)
)
)
# -- Server --
def server(input, output, session):
# store initial defaults
DEFAULTS = {
"A": 1.0,
"A2": 1.0,
"beta": 0.98,
"sigma":2.0,
"Ms": 1.0,
"pi": 0.02
}
# reset sliders to initial defaults when button is pressed
@reactive.event(input.reset)
def _reset_inputs():
for name, val in DEFAULTS.items():
session.set_input_value(name, val)
@output
@render_plot()
def plot():
# Base parameters
A0, A20, beta0, sigma0, Ms0, pi0 = 1.0, 1.0, 0.98, 2.0, 1.0, 0.02
# Current
A, A2, beta, sigma, Ms, pi = (
input.A(), input.A2(), input.beta(), input.sigma(), input.Ms(), input.pi()
)
# Y grid
Y = np.linspace(0.1, 10, 100)
# Compute curves
i_IS_base = [compute_i_IS(y, beta0, A0, A20, pi0, sigma0) for y in Y]
i_LM_base = compute_i_LM(Y, Ms0)
i_IS_cur = [compute_i_IS(y, beta, A, A2, pi, sigma) for y in Y]
i_LM_cur = compute_i_LM(Y, Ms)
# Equilibrium for current
eq_diff = np.abs(np.array(i_IS_cur) - np.array(i_LM_cur))
idx = eq_diff.argmin()
Y_eq, i_eq = Y[idx], i_IS_cur[idx]
# Plot
fig, ax = plt.subplots(figsize=(8,6))
# base curves
ax.plot(Y, i_IS_base, '--', color='gray', alpha=0.5, label='IS (base)')
ax.plot(Y, i_LM_base, '--', color='gray', alpha=0.5, label='LM (base)')
# current curves
ax.plot(Y, i_IS_cur, '-', color='crimson', label='IS (current)')
ax.plot(Y, i_LM_cur, '-', color='navy', label='LM (current)')
# equilibrium
ax.plot(Y_eq, i_eq, 'ko')
ax.axhline(i_eq, linestyle='--', color='black')
ax.axvline(Y_eq, linestyle='--', color='black')
ax.text(Y_eq, i_eq, f' (Y*, i*)=({Y_eq:.2f},{i_eq:.2f})')
ax.set_xlabel('Output Y')
ax.set_ylabel('Interest rate i')
ax.set_title('Exact IS-LM Curves')
ax.legend()
ax.grid(True)
return fig
app = App(app_ui, server)Exercice 4 – Inflation future et inflation présente
Dans un cadre néo‑keynésien à prix rigides, \(\pi_1\) est l’inflation entre t=0→1, \(\pi_2\) entre 1→2, toutes deux exogènes. Si \(\pi_2\) augmente (ex. hausse de \(M^s\)), que fait \(\pi_1\) ? Décrivez les étapes du raisonnement.
Exercice 5 – Politique budgétaire vs. politique monétaire
Guerre chars USA vs Canada, prix rigides.
- Si la Fed garde \(M^s\) constant :
- Effet sur \(Y\) ?
- Sur taux nominaux \(i\) ?
- Sur niveau des prix \(P\) ?
- Effet sur \(Y\) ?
- Si la Fed ajuste \(M^s\) pour maintenir \(i\) constant :
- Que fait‐elle sur \(M^s\) ?
- Impact sur \(Y\) vs (1) ?
- Impact sur \(P\) vs (1) ?
- Que fait‐elle sur \(M^s\) ?
- Si la Fed cible strictement \(\pi\) :
- Que fait‐elle sur \(M^s\) ?
- Impact sur \(Y\) vs (1) ?
- Impact sur \(i\) vs (1) ?
- Que fait‐elle sur \(M^s\) ?
Exercice 6 – Consommation patriotique
Le Président appelle à consommer, un ménage achète une tondeuse.
- Proposez un modèle où cet appel nuit au bien‑être. Décrivez précisément le mécanisme.
- Proposez un modèle où cet appel est bénéfique. Décrivez précisément le mécanisme.
Exercice 7 – Impôts et inflation
Prix rigides, la Fed ne bouge pas. Deux impôts temporaires rapportant même recette :
- Forfaitaire \(\Delta\) par ménage
- Taxe proportionnelle à la consommation
- Si \(G_{t}\) et \(G_{t+1}\) inchangés, à quoi les ménages s’attendent‑ils pour \(T_{t+1}\) ?
- L’un ou l’autre plan réduit‑il \(\pi\) ? Quel canal ? Sinon, pourquoi ?
- Si beaucoup de ménages sont contraints par leur accès au crédit, quel impact sur votre réponse ?
Papier scientifique de la semaine
