Cycles économiques
TD Introduction à la macroéconomie
2025-04-15
Rappels de cours
Cycles d’affaires réels
\[\begin{align} \max_{c_1, c_2, l, L, K} \quad & u(c_1) + v(l) + \beta u(c_2) \\ \text{s.t.} \quad & c_1 + K = Y_1 \\ & Y_1 = F_1(L) \\ & c_2 = F_2(K) \\ & L = 1 - l \end{align}\]
Cycles d’affaires réels
\[Y_1 = F_1(L)\]
\[\frac{v'(1-L)}{u'(c_1)} = F'_1(L)\]
\[u'(c_1) = \beta F'_2(K)u'(F_2(K))\]
\[Y_1 = (u')^{-1}[\beta F'_2(K)u'(F_2(K))] + K\]
Cycles d’affaires réels
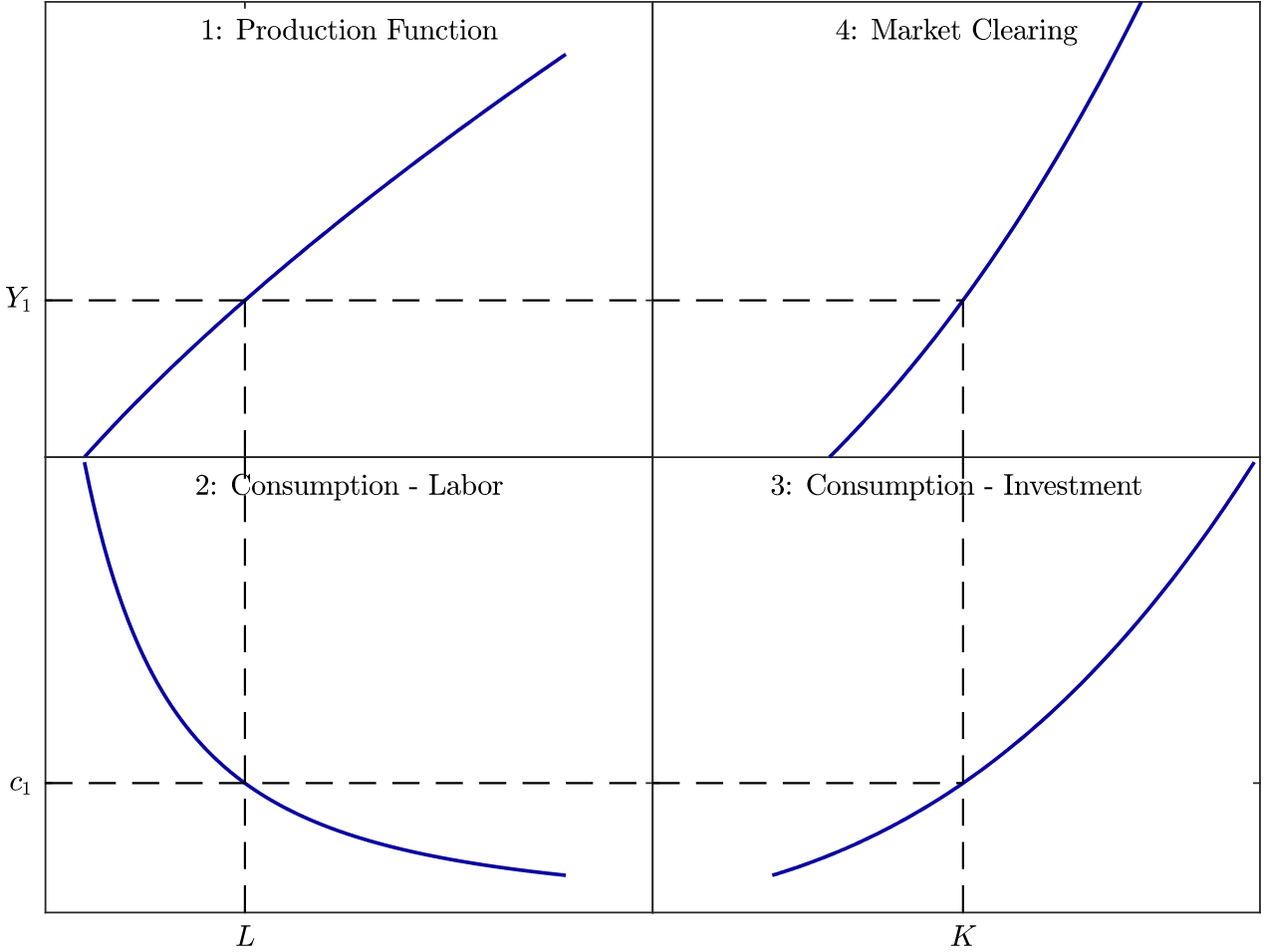
Exercice 1 - Stabiliser une économie très volatile
Vous allez refaire le calcul de Lucas pour une économie constamment confrontée à la Grande Dépression. Consultez les données du PIB des Etats Unis pour 1929 (le pic avant la Grande Dépression) et 1933 (le creux de la Grande Dépression)[slide 16 chapitre 12]. Imaginez une économie où la consommation est la moitié du temps au niveau de 1929 et l’autre moitié au niveau de 1933.
Quelle est la valeur de \(f\) ? Supposez \(u(c) = \frac{c^{1-\sigma}}{1-\sigma}\), donc \[W(c_0, g, f) = \sum_{t=0}^{\infty} \beta^t \left[ \frac{1}{2} u(c_0(1+g)^t(1+f)) + \frac{1}{2} u(c_0(1+g)^t(1-f)) \right]\] \[= \frac{1}{2(1-\sigma)} c_0^{1-\sigma} \frac{(1+f)^{1-\sigma}+(1-f)^{1-\sigma}}{1-\beta(1+g)^{1-\sigma}}\]
Quelle est la valeur, pour le ménage représentatif de cette économie, d’une stabilisation complète de la consommation au niveau moyen ? Essayez les valeurs suivantes de \(\sigma\) : 2, 5 et 10.
Exercice 2 - L’hétérogénéité et la valeur de la stabilisation
Imaginez une économie qui passe la moitié du temps en récession et l’autre moitié en expansion. Dans cette économie, on distingue deux types de ménages : les ménages stables et les ménages volatils. Les ménages stables consomment \(c\) à chaque période, ce qui les rend insensibles au cycle économique. Les ménages volatils consomment : \[c_t^v = \begin{cases} c(1+v) & \text{en période d'expansion} \\ c(1-v) & \text{en récession} \end{cases}\]
Supposez qu’une fraction \(\mu\) des ménages de l’économie soit volatile et qu’une fraction \(1-\mu\) soit stable. Supposez \(u(c) = \frac{c^{1-\sigma}}{1-\sigma}\).
- Quelle est la consommation totale dans l’économie, respectivement en période d’expansion et de récession ?
Pour les questions restantes, supposons \(\sigma = 5\), \(f = 0,012\) et \(\mu = 0,05\).
Supposons que la consommation globale soit bien décrite par l’équation en bas de la slide 18 (chap 12). Étant donné une valeur de \(\mu\), quelle valeur de \(v\) entraînerait des fluctuations de la consommation globale d’amplitude égale à \(f\) ?
Quelle est la valeur pour un ménage stable de l’élimination du cycle économique ?
Quel est l’intérêt pour un ménage volatil de supprimer le cycle économique ?
Quel est l’intérêt de supprimer le cycle économique pour un ménage qui, derrière le voile de l’ignorance, n’est pas sûr de sa stabilité ou de sa volatilité ?
Exercice 3 - Les prix dans le modèle RBC
Considérez le modèle RBC à deux périodes, résumé par les équations (1) à (4) [slide 4 chap 13].
Supposons un choc de productivité positif et temporaire uniquement à la période 1. Qu’advient-il du salaire \(w\) et du taux d’intérêt réel \(r\) ? Expliquez pourquoi chacun des prix varie.
Supposons une augmentation temporaire de la préférence des ménages pour les loisirs. Qu’advient-il du salaire \(w\) et du taux d’intérêt réel \(r\) ? Expliquez pourquoi chacun des prix varie.
Exercice 4 - Stabilisation un cycle économique réel
Supposez que l’économie soit bien décrite par le modèle du cycle économique réel. L’économie vient de subir un choc positif sur la productivité globale.
Supposez que le gouvernement souhaite que le PIB reste au même niveau qu’il aurait été sans le choc de productivité. Décrivez un instrument politique possible à cet effet. Expliquez son efficacité.
Supposez plutôt que le gouvernement souhaite que l’emploi reste au même niveau qu’il aurait été sans le choc de productivité. La politique doit-elle être appliquée plus ou moins intensément ? Pourquoi ?
Exercice 5 - Bonne nouvelle
Considérez le modèle RBC à deux périodes, résumé par les équations (1) à (4). Supposez que le ménage représentatif développe une forme très particulière d’optimisme quant à l’avenir. Il estime que la fonction de production de la période 2 est :
\[Y_2 = F_2(K) + A\]
En quoi ce type d’optimisme diffère-t-il de celui étudié en cours ?
Qu’adviendra-t-il de l’emploi, de la production, de la consommation, de l’investissement, des salaires et du taux d’intérêt réel ?
Ce type d’optimisme produit-il quelque chose qui ressemble à un cycle économique? Pourquoi ?
Exercice 5 - Bonne nouvelle
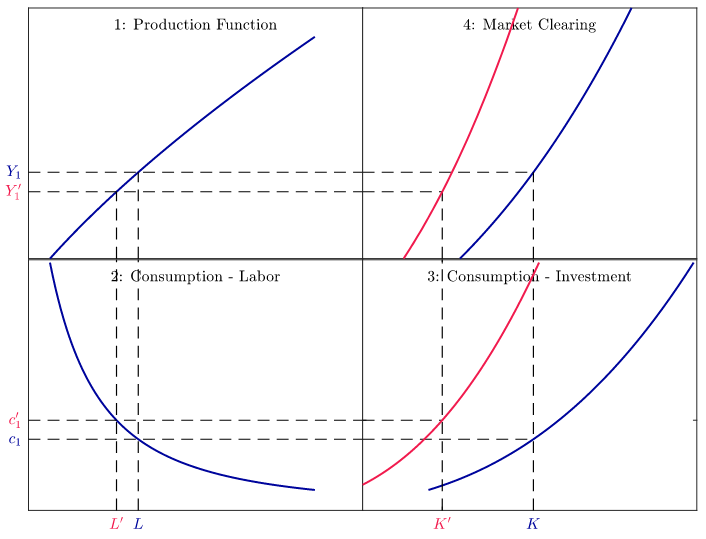
Exercice 6 - Dépenses publiques
Considérez une économie bien décrite par le modèle RBC, avec une modification près : un gouvernement dépense \(G\) à la période 1. Il finance ces dépenses en prélevant des impôts forfaitaires auprès du ménage représentatif (l’équivalence ricardienne est vérifiée, il n’est donc pas nécessaire de préciser quand le gouvernement perçoit ces impôts). G n’entre pas dans la fonction d’utilité du ménage représentatif.
Où \(G\) apparaîtrait-il dans le système d’équations (1)-(4) ? Expliquez.
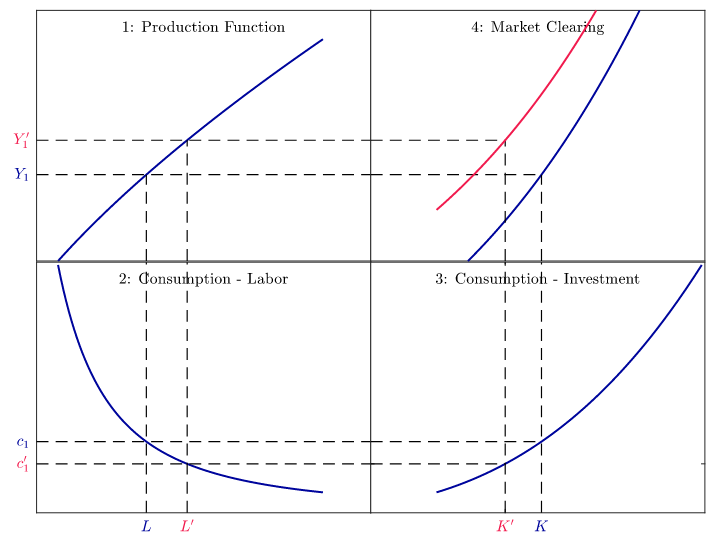
Supposez une augmentation de \(G\). Qu’advient-il de la production, de la consommation, de l’emploi et de l’investissement ? Qu’advient-il des salaires et des taux d’intérêt ? Représentez-le graphiquement et expliquez ce qui se passe.
Exercice 6 - Dépenses publiques
Papier scientifique de la semaine
