Faits de Kaldor et modèle de Solow Pt1

TD Introduction à la macroéconomie

Kilian Rouge

CIRED

2025-02-11

Rappels de cours

Les faits de Kaldor

Fait de Kaldor	Équation
1. Le taux de croissance du PIB/hab est constant.	\(\frac{d(\frac{Y}{L})}{dt} = g\)
2. Le ratio du stock de capital total au PIB est constant.	\(\frac{K}{Y} = c\)
3. Les parts des revenus du travail et du capital dans le PIB sont constantes.	\(\frac{W}{Y} = \theta_L \quad \text{et} \quad \frac{R}{Y} = \theta_K\)
4. Le taux de rendement du capital est constant.	\(r = \frac{\partial Y}{\partial K} = c\)

Remise en question des faits de Kaldor

Dynamique économique	Explication	Faits de Kaldor impactés
Transition vers un capital intangible et financier	Le capital immatériel et la financiarisation augmentent le ratio \(\frac{K}{Y}\) sans refléter une production réelle, maintenant un rendement élevé du capital.	2, 4
Croissance économique plus faible	La croissance ralentie dans les économies avancées augmente l’accumulation de capital, faisant diverger le rendement du capital du taux de croissance économique.	1, 2, 4
Part des revenus du capital en hausse	La part croissante des revenus du capital, soutenue par la financiarisation et des politiques fiscales favorables, remet en cause la répartition factorielle de Kaldor.	3
Mobilité des capitaux et optimisation fiscale	L’optimisation fiscale et la mondialisation redirigent les investissements vers des secteurs à rendements élevés, modifiant les rendements du capital.	4
Innovation et progrès technique	Les innovations et l’automatisation ne compensent pas systématiquement les rendements décroissants du capital, changeant les dynamiques de production et de répartition.	1, 4

Schéma du modèle: Construction

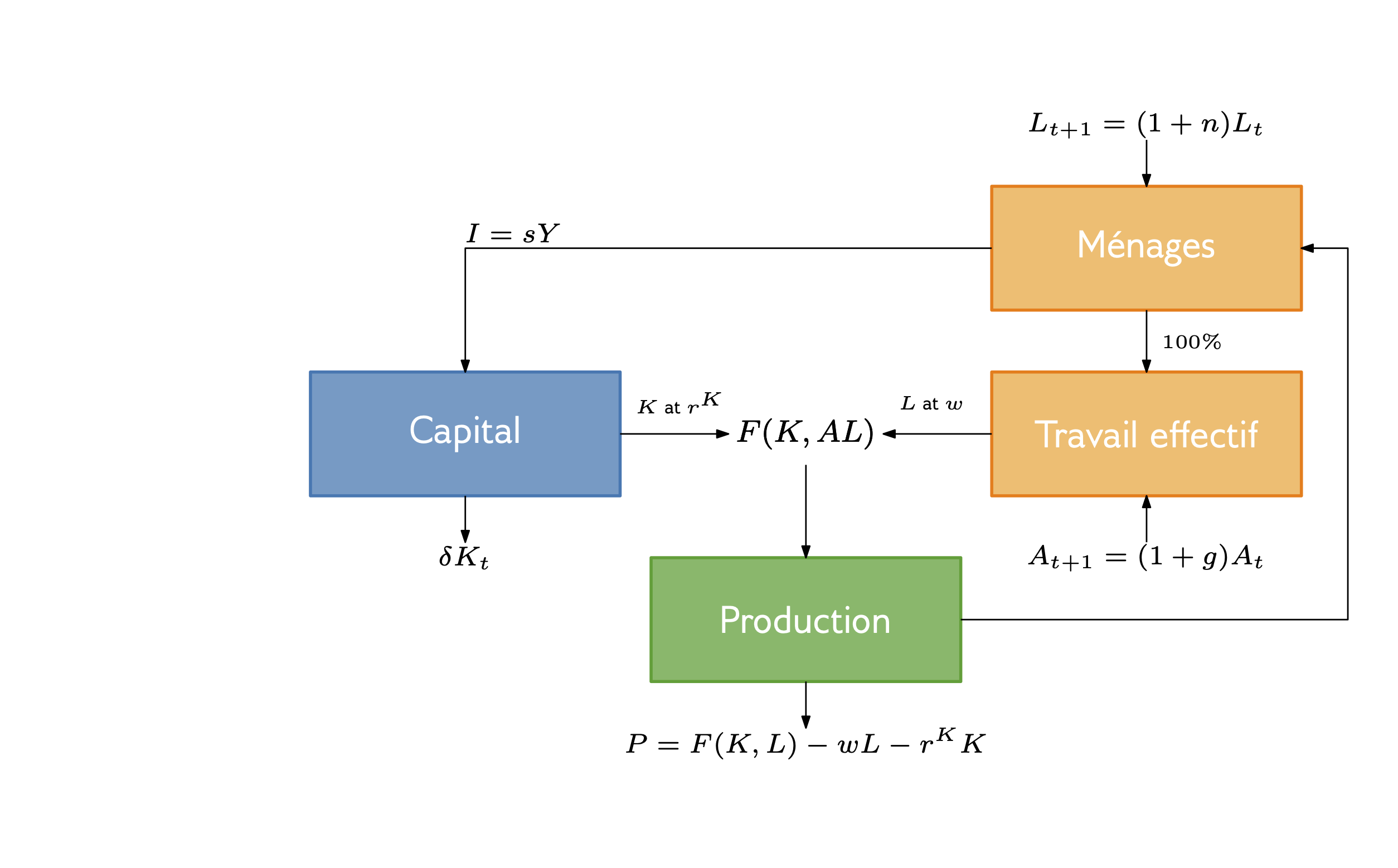
Schéma du modèle: Résultats

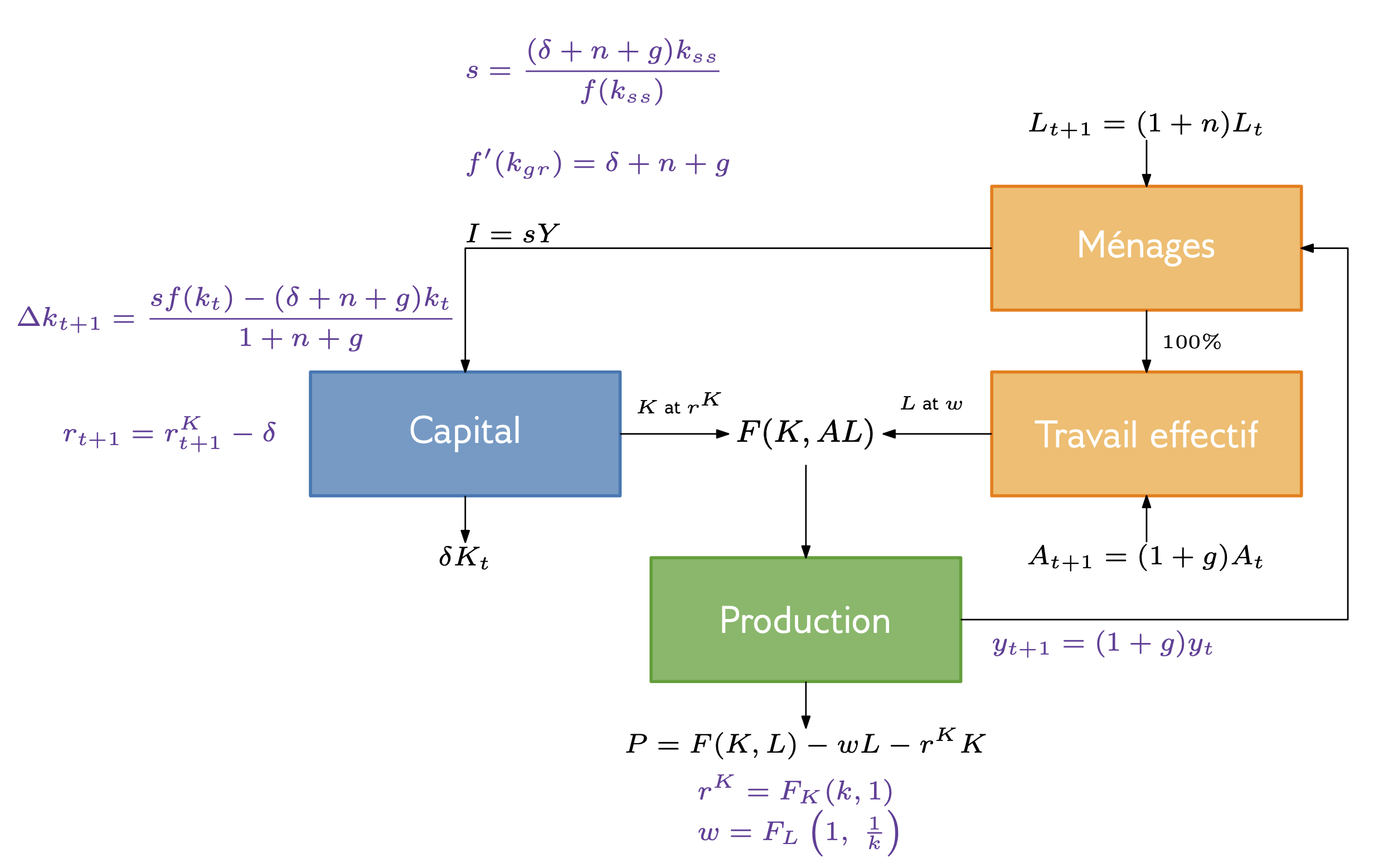
Dynamiques du modèle de Solow

#| '!! shinylive warning !!': |
#|   shinylive does not work in self-contained HTML documents.
#|   Please set `embed-resources: false` in your metadata.
#| standalone: true
#| viewerHeight: 550

import numpy as np
import matplotlib.pyplot as plt
from shiny import App, ui, render

# Cobb-Douglas production function
def cobb_douglas(k, alpha):
    return k ** alpha

# Solow model functions with technological progress
def output_per_worker(k, alpha):
    return cobb_douglas(k, alpha)

def savings_per_worker(k, alpha, s):
    return s * cobb_douglas(k, alpha)

def depreciation_per_worker(k, delta, n, g):
    return (delta + n + g) * k

# Function to find equilibrium point
def find_equilibrium(alpha, s, delta, n, g):
    k_eq = (s / (delta + n + g)) ** (1 / (1 - alpha))
    y_eq = cobb_douglas(k_eq, alpha)
    return k_eq, y_eq

app_ui = ui.page_fluid(
    ui.layout_sidebar(
        ui.sidebar(
            ui.input_slider("alpha", "Alpha", min=0.1, max=0.5, value=0.3, step=0.01),
            ui.input_slider("s", "Savings Rate (s)", min=0.1, max=0.5, value=0.2, step=0.01),
            ui.input_slider("delta", "Depreciation Rate (δ)", min=0.01, max=0.1, value=0.05, step=0.01),
            ui.input_slider("n", "Population Growth (n)", min=0.01, max=0.1, value=0.02, step=0.01),
            ui.input_slider("g", "Tech Progress (g)", min=0, max=0.1, value=0.02, step=0.01)
        ),
        ui.output_plot("plot"),
    ),
)

def server(input, output, session):
    # Store previous values
    prev_values = {"alpha": None, "s": None, "delta": None, "n": None, "g": None}

    @output
    @render.plot
    def plot():
        # Get current values
        alpha = input.alpha()
        s = input.s()
        delta = input.delta()
        n = input.n()
        g = input.g()

        k = np.linspace(0.01, 10, 1000)
        y = output_per_worker(k, alpha)
        sfk = savings_per_worker(k, alpha, s)
        dnk = depreciation_per_worker(k, delta, n, g)
        k_eq, y_eq = find_equilibrium(alpha, s, delta, n, g)

        fig, ax = plt.subplots(figsize=(10, 6))

        # Plot previous values if available (without labels)
        if prev_values["alpha"] is not None:
            prev_y = output_per_worker(k, prev_values["alpha"])
            prev_sfk = savings_per_worker(k, prev_values["alpha"], prev_values["s"])
            prev_dnk = depreciation_per_worker(k, prev_values["delta"], prev_values["n"], prev_values["g"])
            prev_k_eq, prev_y_eq = find_equilibrium(
                prev_values["alpha"], prev_values["s"],
                prev_values["delta"], prev_values["n"], prev_values["g"]
            )

            ax.plot(k, prev_y, color='lightblue', alpha=0.5)
            ax.plot(k, prev_sfk, color='lightgreen', alpha=0.5)
            ax.plot(k, prev_dnk, color='pink', alpha=0.5)
            ax.scatter([prev_k_eq], [prev_y_eq], color='purple', alpha=0.3, s=100)
            ax.vlines(prev_k_eq, 0, prev_y_eq, colors='purple', alpha=0.3, linestyles='--')
            ax.hlines(prev_y_eq, 0, prev_k_eq, colors='purple', alpha=0.3, linestyles='--')

        # Plot current values
        ax.plot(k, y, color='blue', label='y = f(k)')
        ax.plot(k, sfk, color='green', label='s * f(k)')
        ax.plot(k, dnk, color='red', label='(δ + n + g) * k')
        ax.scatter([k_eq], [y_eq], color='purple', s=100, label='Equilibrium Point')
        ax.vlines(k_eq, 0, y_eq, colors='purple', linestyles='--')
        ax.hlines(y_eq, 0, k_eq, colors='purple', linestyles='--')

        ax.set_title('Solow Model with Technological Progress')
        ax.set_xlabel('Capital per Effective Worker (k)')
        ax.set_ylabel('Output per Effective Worker (y)')
        ax.grid(True, alpha=0.3)
        ax.legend(loc='lower right')

        # Update previous values
        prev_values.update({
            "alpha": alpha,
            "s": s,
            "delta": delta,
            "n": n,
            "g": g
        })

        return fig

app = App(app_ui, server)

Socle d’hypothèses du modèle de Solow

#	Hypothèse	Critique
	Hypothèses néoclassiques courantes
1	Fonction de production	Substitution capital/travail complexe, Caractéristiques fonctionnelles
2	Rendements d’échelle constants, productivité marginale décroissante	Rendements croissants; Hypothèse capital homogène
3	Concurrence parfaite	Valable à long terme; contestée à court terme
4	Absence d’intervention gouvernementale	Inadéquat depuis la crise de 29
	Hypothèses spécifiques à Solow
5	Économie fermée	Omet les effets du commerce international
6	Homogénéité du travail et du capital	Controverse des 2 Cambridge
7	Plein emploi du travail et du capital	Plein emploi du travail discutable
8	Bien homogène	Simplification acceptable
9	Proportion fixe du revenu investie	Taux d’épargne relativement stable

TD

Exercice 1

À partir de 1800, recherchez le PIB américain par habitant à intervalles d’une décennie. Pour chacun de ces moments, trouvez le pays dont le PIB par habitant est actuellement le plus proche du niveau passé des États-Unis. Quand les États-Unis sont-ils devenus plus riches que l’Inde, la Chine et la France d’aujourd’hui ?

# Select US GDP per capita per year 🛠️
us_data = data[data['country'] == 'United States'][['year', 'gdppc']]

# Extract GDP per capita for the United States at decade intervals from 1800
us_gdp_decades = us_data[(us_data['year'] >= 1800) & (us_data['year'] % 10 == 0)]
us_gdp_decades

Exercice 1

	year	gdppc
124713	1800	2545.488000
124723	1810	2725.472000
124733	1820	2674.048000
124743	1830	3039.158400
124753	1840	3319.419200
124763	1850	3631.820000
124773	1860	4401.894400
124783	1870	4803.001600
124793	1880	6255.729600
124803	1890	6664.550400
124813	1900	8037.571200
124823	1910	9636.782722
124833	1920	10152.927109
124843	1930	10694.982075
124853	1940	12005.095163
124863	1950	15240.000000
124873	1960	18057.000000
124883	1970	23958.000000
124893	1980	29611.000000
124903	1990	36982.000000
124913	2000	45886.470498
124923	2010	49266.915862
124933	2020	54379.206512

Exercice 1

# Get the most recent GDP per capita data for all countries
latest_year = data['year'].max()
latest_gdp = data[data['year'] == latest_year][['country', 'gdppc']]

# List to store the results
closest_countries = []

# Find the country with the closest GDP per capita for each decade 🛠️
for decade in us_gdp_decades["year"]:
    gdp_diff = float('inf')
    closest_country = None
    us_gdp = us_gdp_decades[us_gdp_decades["year"] == decade]["gdppc"].values[0]
    for country in latest_gdp["country"]:
        country_gdp = latest_gdp[latest_gdp["country"] == country]["gdppc"].values[0]
        test_gdp_diff = abs(country_gdp - us_gdp)
        if test_gdp_diff < gdp_diff:
            gdp_diff = test_gdp_diff
            closest_country = country
    closest_countries.append((decade, us_gdp, closest_country, gdp_diff))

# Convert the results to a DataFrame
closest_countries_df = pd.DataFrame(closest_countries, columns=['Year', 'US GDP per Capita', 'Closest Country', 'GDP Difference'])
closest_countries_df

Exercice 1

	Year	US GDP per Capita	Closest Country	GDP Difference
0	1800	2545.488000	Syrian Arab Republic	50.726705
1	1810	2725.472000	Senegal	64.790275
2	1820	2674.048000	Senegal	13.366275
3	1830	3039.158400	U.R. of Tanzania: Mainland	18.170325
4	1840	3319.419200	Zambia	23.002125
5	1850	3631.820000	Djibouti	8.759756
6	1860	4401.894400	Ghana	159.483731
7	1870	4803.001600	State of Palestine	27.799541
8	1880	6255.729600	Angola	136.824703
9	1890	6664.550400	Republic of Moldova	10.320888
10	1900	8037.571200	Viet Nam	12.787631
11	1910	9636.782722	El Salvador	417.877223
12	1920	10152.927109	Ecuador	28.850547
13	1930	10694.982075	Sri Lanka	10.499408
14	1940	12005.095163	Bosnia and Herzegovina	137.768038
15	1950	15240.000000	Costa Rica	256.820571
16	1960	18057.000000	Argentina	235.317825
17	1970	23958.000000	Panama	400.980446
18	1980	29611.000000	Hungary	159.144213
19	1990	36982.000000	Israel	333.083045
20	2000	45886.470498	Canada	356.824890
21	2010	49266.915862	Netherlands	402.952693
22	2020	54379.206512	Saudi Arabia	862.297475

Exercice 1

# Determine when the US became richer than India, China, and France of today 🛠️
india_gdp = latest_gdp[latest_gdp['country'] == 'India']['gdppc'].values[0]
china_gdp = latest_gdp[latest_gdp['country'] == 'China']['gdppc'].values[0]
france_gdp = latest_gdp[latest_gdp['country'] == 'France']['gdppc'].values[0]

richer_than_india = us_gdp_decades[us_gdp_decades['gdppc'] > india_gdp].iloc[0]['year']
richer_than_china = us_gdp_decades[us_gdp_decades['gdppc'] > china_gdp].iloc[0]['year']
richer_than_france = us_gdp_decades[us_gdp_decades['gdppc'] > france_gdp].iloc[0]['year']

# Print the results
print(f"\nThe US became richer than India of today in: {richer_than_india}")
print(f"The US became richer than China of today in: {richer_than_china}")
print(f"The US became richer than France of today in: {richer_than_france}")


The US became richer than India of today in: 1900.0
The US became richer than China of today in: 1970.0
The US became richer than France of today in: 2000.0

Exercice 4 - Un tremblement de terre

Supposons qu’une économie se comporte selon le modèle de croissance de Solow. Cela commence à \(t = 0\) dans un état stable, sans progrès technologique ni croissance démographique. Supposons qu’un tremblement de terre détruise la moitié du stock de capital. En conséquence,

Que se passerait-il à court terme (c’est-à-dire immédiatement) et à long terme (c’est-à-dire une fois que l’économie aurait atteint l’état stationnaire) pour :

le PIB,
le PIB par habitant,
les salaires,
le taux d’intérêt.

Exercice 5 - La peste noire

Au milieu du XIVe siècle, une peste a tué environ un tiers de la population européenne. Supposons que l’économie européenne ait été bien décrite par le modèle de Solow. Comment les variables suivantes changeraient-elles en réponse à la peste noire à court terme (c’est-à-dire immédiatement) ?

le PIB,
le PIB par habitant,
les salaires,
le taux d’intérêt.

Papier scientifique de la semaine